God Time = Planck Time: Finally Detected! And Its Relation to Hubble Time

Espen Gaarder Haug

Handelshøyskolen, Norwegian University of Life Science, Ås, Norway.

DOI: 10.4236/ojm.2024.142004                

Abstract

Newton already mentioned indivisible time in Principia. In 1899, Max Planck derived a unique time period from three universal constants: G, c, and ħ, and today this is known as the Planck time. The Planck time is of the order of about 10⁻⁴⁴ seconds while the best atomic clocks are down to 10⁻¹⁹ seconds. An approach has recently been outlined that puts an upper limit on the quantization of time to 10⁻³³ seconds; this is, however, still far away from the Planck time. We demonstrate that the Planck time can easily be measured without any knowledge of any other physical constants. This is remarkable as this means we have demonstrated that the Planck time and therefore the Planck scale is real and detectable. It has taken more than 100 years to understand this. The reason for the breakthrough in Planck scale physics in recent years comes from understanding that G is a composite constant and that the true matter wavelength is the Compton wavelength rather than the de Broglie wavelength. When this is understood, the mysteries of the Planck scale can be uncovered. In this paper, we also demonstrate how to measure the number of Planck events in a gravitational mass without relying on any constants. This directly relates to a new and simple method for quantizing general relativity theory that we also will shortly discuss.

Keywords

Planck Time, Fundamental Time, Indivisible Time, Newton, Planck Length, Quantum Gravity

1. The Early Forgotten History of the Indivisible Time Interval

The Higgs boson was popularized partly because it was coined The God Particle, due to Nobel Laureate Lederman’s [1] 1993 book with the same title about concepts related to the Higgs boson. Many physicists did not like the label The God Particle for the Higgs boson, but it is still often used. On the other hand, we see, surprisingly, that the possible first mention of an indivisible time interval seems to have been in the bible; something we soon will get back to. We are not mentioning this because we want to mix religion and physics, but simply because it is an interesting historical fact that has typically gone unnoticed.

Isaac Newton [2] in his 1686 book Principia wrote:

Since every particle of space is always and every indivisible moment of duration is everywhere certainly the Maker and Lord of all things cannot be never and nowhere…”. Further, he mentioned: “…then we conclude the least particles of all bodies to be also extended, and hard and movable, and endowed with their proper vires inertia. And this is the foundation of all philosophy.—Isaac Newton (p. 505).

Newton clearly mentioned an indivisible time interval. If a time interval is indivisible, it cannot be broken down further and cannot be shorter. That Newton mentions an indivisible time interval has basically gone unnoticed by the physics community. It could naturally be that Newton came up with the idea of indivisible time himself, but he is mixing this in with some “religious talk” which was not uncommon among scientists back then. It is also well known that Newton, in addition to his physics, spent considerable time reading scriptures as well as the bible; some say in the hope of finding deeper and ancient wisdom, or perhaps to please the church; see, for example, Heberle-Bors [3] for a discussion on this. Interestingly, the first place an indivisible time interval is mentioned is in the New Testament (in Paul’s 1 Corinthians 15:52. In the original Greek version, we find

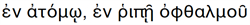
This has often been translated in the English translation of the New Testament as “In an instant, in the twinkling of an eye”. But we think all English translations we have seen miss an important point. “ατoμoν” is ancient Greek that in English means atom, and atom in ancient Greek means indivisible, or uncuttable, that is, something that cannot be divided further. So “atomic time” must, in our interpretation, have meant an indivisible time interval—not only an instant—and the difference in interpretation is large. The word “atom” meant indivisible particle since the time of Democritus, and Leuppicus [4] [5] introduced atomism about 500 B.C.

The famous theologian and philosopher, Saint Augustine, as cited in [6] , was clear in interpreting this passage from Paul’s 1 Corinthians as representing indivisible time. Saint Augustine lived from the year 354 to 430 AD and was also clear that many, even back then, did not know what an atom was, as they were not familiar with the subject. For example, St. Augustine wrote,

“A year, for example, is split into months, months are divided into days, and days can be split into hours and now hours can be lead into certain parts of hours which admit division, up until you arrive at such point in time and a certain droplet of moment so that no further parts can be drawn out of it and so it cannot be divided: this is the atom in time.”—Saint Augustine

Bede, who wrote a text titled “De Temporum Ratione” related to the calculation of Easter and published in the year 703 AD, specifically referred to Paul’s 1 Corinthians and again interpreted it as a time interval that cannot be divided [7] [8] .

However, as one delves deeper into the Middle Ages, the precise interpretation of atomic time becomes less clear. We believe this ambiguity is largely due to part of the Catholic Church’s opposition to atomism back then. For instance, Rabanus Maurus (780-856) abruptly redefined atomic time as merely the duration of an eye’s twinkle. Over time, the interpretation held by theological and philosophical experts—that atomic time represents the shortest possible indivisible time interval—lost its significance and was likely misinterpreted. Later, as Latin fell out of use, the English translation of the New Testament failed to convey the concept that atomic time probably meant indivisible time. The Catholic Church’s hostility towards atomism persisted at least until the Renaissance and Early Modern Era. For example, in 1624, the Paris Parliament decreed that anyone advocating or teaching atomism would be subject to the death penalty. Parisian scholars Bitaud and de Villion, who attempted to demonstrate atomism (indivisibles) through experiments, were arrested by the police for their efforts. According to more recent research by Redondi [9] , the Galileo affair was primarily about Galileo violating the Catholic Church’s prohibition on discussing atomism. This naturally has little to do with any specific religion but rather with how various powers at different times in history have suppressed free speech and the flow of ideas. That some organizations at certain points in time have suppressed ideas does not mean they have not also come up with great discoveries. For example, thanks to discoveries by the Catholic priest Lemaître [10] , who was the first to estimate what is now known as the Hubble constant, his work complemented that of Hubble [11] , resulting in considerably improved insight about the cosmos today. As we will soon describe, the concept of God-Time (indivisible) is even concealed within the Hubble constant.

Still everyone knew that atom meant indivisible all the way up to the time when John Dalton introduced the periodic system in 1808. Dalton thought he had found the indivisible particles of the Greek philosophers, but some years later it was shown that what he thought were atoms (indivisibles) where composite particles, in other words, divisible. However, the word “atom” was maintained for these elements that had nothing to do with the original meaning of the word. Several scientists in the past did, in fact, point out that the Daltonian atom was not a true atom (an indivisible), even before this was fully proven. For example, in their book A History of Science, published in 1904, Williams and Williams [12] stated that:

There are, indeed, as we shall see, experiments that suggest the dissolution of the [Dalton] atom—that suggest, in short, that the Daltonian atom is misnamed, being a structure, under certain conditions, be broken asunder. When experiment shall have demonstrated the Daltonian atom is a compound, and that in truth there is a single true atom, which, combining with its fellows perhaps in varying numbers and in different special relations, produces the Daltonian atoms, then the philosophical theory of monism will have the experimental warrant which to-day it lacks.

Gæury [13] points out that even if time is mentioned by Epicurus (another atomist) it is never mentioned explicit that also time is thought of as indivisible in his atomism. However, Gæury indicates that still this was indirectly clear.

Moses Maimonides [14] in his book “A Guide for the Perplexed” published around year 1190 describes that “Time is composed of time-atoms” where he further go on to discuss indivisible time units. He even goes on to say that the shortest time unit is of the order to take the shortest common time unit and divide by 60 ten times in a row. If the shortest standard time unit was a blink of an eye which is about a tenth of a second, then this time unit would be of the order of 10⁻¹⁹ seconds. This is far above the Planck time, but still an impressive speculative guess of the ultimate shortest time interval. Isaac Newton supposedly had the book of Maimonides and even made notes about it, so possibly also Newton got the idea of indivisible time from Maimonides.

Our point is that until Dalton the word “atom” was always interpreted as indivisible, the true ancient Greek meaning of the word. So, we are quite convinced that the original New Testament talked about an indivisible time and not just an instant, or a short time interval. The indivisible time is, however, according to recent findings, the Planck time, so it is also an instant, or the shortest possible instant of time that exists. Yet, to call it just an instant of time is an incomplete description. Indivisible (atomic) time, on the other hand, gives a complete description of perhaps one of the most important things in physics. An instant period is just a very short time period; it could even be a second or a millisecond. Naturally other time units existed back then as the second were not yet invented. Atom (indivisible) time on the other hand is the very shortest time interval that can exist, so it is likely linked to the very foundation of time.

One possibility, and we would even say a likelihood, is that Isaac Newton therefore had the idea of indivisible time from the New Testament, when he mentioned indivisible time in his book Principia. This we will likely never know for sure; what we do know is that Isaac Newton studied the Bible in detail. Newton likely reading the Greek version; in his time the word “atom” was not misinterpreted, at least not by scientists, as the only meaning of the word then was indivisible. It was first with Dalton that the word “atom” lost its original meaning when attached to elements which he thought were indivisibles, but which were actually divisible composite particles.

2. Planck Time, Quantum Time, and Quantum Gravity

In 1899 Max Planck [15] [16] introduced a unique length: $l_p=\sqrt{\frac{G\hslash }{c^3}}$ , time: $t_p=\sqrt{\frac{G\hslash }{c^5}}$ , mass: $m_p=\sqrt{\frac{\hslash c}{G}}$ and temperature: $T_p=\frac{1}{k_b}\sqrt{\frac{\hslash c^5}{G}}$ . Planck got to these by assuming there were three important universal constants: the gravitational constant G, the Planck constant h, and the speed of light, then he combined these with dimensional analysis one get these units. These units are today known as the Planck units [17] or just natural units. However, until recently, it has been assumed it is almost impossible to detect the Planck scale (see for example [18] [19] [20] ) and therefore also to measure the Planck time. For example, the most accurate atomic and optical clocks can measure a time interval of about 10⁻¹⁹ seconds; see [21] . Wendel, Martínez, and Bojowald [22] who have recently found a strong upper boundary of the fundamental period of time of approximately 10⁻³³ seconds, which is still not even close to the Planck time that is only approximately:

$t_p=\sqrt{\frac{G\hslash }{c^5}}=\frac{l_p}{c}\approx 5.4\times {10}^{-44}\text{s}$

The Planck time is, by most physicists [23] [24] , considered the shortest possible, even hypothetically measurable, time interval. Some think it is an invariant indivisible time interval. The Planck time is the time it takes for the speed of light to travel the Planck length, and the Planck length is, among most physicists, considered the minimum length interval, and some even think it is an indivisible length. The reduced Compton wavelength of a Planck mass is the Planck length: $\bar{\lambda }=\frac{\hslash }{m_{p}c}=l_p$ . A better understanding of the Planck time and the other Planck units can be an important step towards a unified quantum gravity theory. Ball [25] summarized nicely in one sentence the importance of better understanding the Planck time:

A physics to match the Planck timescale is the biggest challenge to physicists in the coming century.—Philip Ball, 1999

This because the Planck time scale (the Planck length, the Planck time, and other Planck units) are likely linked to quantum gravity that is needed to unify gravity with quantum mechanics; see, for example [26] [27] .

In 1984, Cohen suggested that the Planck units were likely more important than the gravitational constant and that the gravitational constant perhaps therefore could be expressed as $G=\frac{\hslash c}{m_p^2}$ , which is simply the Planck mass formula solved with respect to G. However, in 1987, Cohen [28] pointed out that no one had shown a way to find the Planck mass or any other Planck units without first knowing G, so that to express G from Planck units would just lead to a circular problem. This view has been held until very recently and was, for example, repeated in 2016 by McCulloch [29] who also expressed the Newton gravitational constant as $G=\frac{\hslash c}{m_p^2}$ .

Strehl [30] in 1913 discusses that continuous time do not make sense, and that time come in discrete units that he calls zeit-atome (german for time-atoms). Eddington [31] in 1918 was likely the first to suggest the Planck length would have to play a central role in a future quantum gravity theory, but without suggesting how. Actually, already in 1931, Nobel Laureate Percy Bridgman [32] ridiculed the Planck units. For him, they were more like some artificial mathematical units that simply came out of dimensional analysis from other constants. They were, in his view, likely not linked to anything fundamental physical. We will claim little progress has been made for more than 100 years on the Planck scale, except until very recently.

For example, Das and Modak [33] have as recently as 2021, pointed out what is likely still the main view among physicists in relation to the Planck scale detection:

“The Planck or the quantum gravity (QG) scale, being 16 orders of magnitude greater than the electroweak scale, is often considered inaccessible by current experimental techniques.”

We will claim that the Planck scale being considered inaccessible by current experimental techniques by most of the physics community is simply due to a lack of understanding of the Planck scale and the lack of progress in understanding quantum gravity using standard theory, as well as such failed attempts as super string theory. The reason for this, we will claim, is that very few physicists are still aware of the enormous progress made in relation to the Planck scale in the past few years. This is mostly because research about how to detect and understand the Planck scale has mainly been published in low-ranked journals and in a step-by-step process.

We have, in recent years, demonstrated that the Planck length and other Planck units can remarkably be found without any knowledge off G and h, and even without c; see [34] [35] [36] [37] . This is in strong contrast to what was first pointed out by Cohen and that has been the view until recently, and still is the view among most researchers. What is new in this paper is both a more solid historical background on the indivisible time interval and its link to the Planck time, and also that here we employ even more ways that will show how one can easily measure the Planck time with no prior knowledge of G, ħ or c. That is, one needs to know no constants to measure the Planck time. All we need is to combine two gravitational measurements, as will be demonstrated in the next few sections.

The reason we can easily detect the Planck scale is that quantum gravity is remarkably hidden and already embedded in even Newtonian gravity, not by purpose but by calibration. To detect most gravitational effects is to detect the Planck scale. The reason this has not been discovered until recently is that one has, for more than 100 years, used a somewhat ad hoc inserted gravity constant, namely G, that first came into use in 1873. We have gained a new understanding of the Newton gravitational constant now that we can find the Planck units independent of G, as will be demonstrated below.

3. Compton Wavelength for Any Mass

Essential for a recent breakthrough in understanding the Planck scale has been understanding that the Compton wavelength is likely the true matter wavelength, and that the de Broglie wavelength is likely only a mathematical derivative of the Compton wavelength. Since Einstein was able to describe the photo electronic effect, it has been known that light has particle-wave properties. Louis de Broglie suggested also that matter has a wave property in addition to particle properties; in other words, that matter also has particle wave duality. Broglie suggested in his PhD thesis [38] that he presented in 1923/1924, that the matter wavelength was likely given by:

${\lambda }_b=\frac{h}{mv}$ (1)

or in relativistic form [39]

${\lambda }_b=\frac{h}{mv\gamma }$ (2)

where $\gamma$ as usual is the Lorentz factor, $\gamma =1/\sqrt{1-v^2/c^2}$ .

In 1927, Davisson and Germer [40] reported that they had experimentally observed wavelike properties in electrons. This was quickly interpreted as the de Broglie hypothesis where correct. However, physicists forgot to distinguish between de Broglie’s idea that matter had wavelike properties, which indeed was confirmed, and his formula that gave a precise prediction of the length of these waves. The experiment only confirmed the wavelike properties and not any direct measurement on if the length of these waves were the same as predicted by de Broglie’s formula.

In 1923, Arthur Holley Compton [41] reported that to scatter electrons with photons also led to a wavelength linked to matter, today known as the Compton wavelength, that is given by:

$\lambda =\frac{h}{mc}$ (3)

and the reduced Compton wavelength is given by $\bar{\lambda }=\frac{\lambda }{2\pi }$ .

Compton assumed the electrons, when scattered by photons, were standing still when initially hit by photons. This has recently been extended to also hold true when the electron is initially moving; see [42] . The relativistic Compton wavelength is given by:

$\lambda =\frac{h}{mc\gamma }$ (4)

Now let us compare the de Broglie wavelength with the Compton wavelength. If the particle is at rest, then the de Broglie wavelength is not even mathematically defined as it is not mathematically allowed to divide by zero. Alternatively, one can assume a particle never stands fully still, but still then when v approaches zero the de Broglie wavelength approaches infinite. This has led to absurd predictions, such as an electron is everywhere in the universe at the same time, or until observed. On the other hand, the Compton wavelength is always mathematically well defined, and for an electron it always has a length that is of the order of the atomic scale, which makes sense as the electron is very small.

Pay attention to the fact that the de Broglie wavelength is always equal to the Compton wavelength multiplied by $\frac{c}{v}$ . Why would matter have two different wavelengths and light only one wavelength? In our view, the de Broglie wavelength is nothing more than a mathematical derivative of the true matter wavelength, namely the Compton wavelength; see also [43] [44] . There is nothing mathematically wrong with the de Broglie wavelength; it is just it is a mathematical function of a real physical matter wavelength, and so using it instead of the Compton wavelength will complicate interpretations. Also, the de Broglie wavelength is not valid for rest-mass particles.

It’s also important that any mass, not only an electron, has a Compton wavelength. If we solve the Compton wavelength formula with respect to m, we get:

$m=\frac{h}{\lambda }\frac{1}{c}=\frac{\hslash }{\bar{\lambda }}\frac{1}{c}$ (5)

where ħ is the reduced Planck constant ( $\frac{h}{2\pi }$ ).

To rewrite the Compton wavelength formula in terms of mass is trivial, but it seems it was first done and used in 2018 by Haug [45] . Some will likely protest here and say we cannot simply solve the Compton wavelength formula with respect to m, in particular not for masses that are not electrons. Actually, the idea that also protons have Compton wavelength goes back to at least 1958 with the paper of Levitt [46] , and recently attention to the Compton wavelength of the proton increased; see Bohr and Trinhammer [47] .

We think only fundamental particles have a physical Compton wavelength. Still, all larger masses are composites of fundamental particles, and their aggregates of reduced Compton wavelengths can be found by the following aggregation formula:

$\bar{\lambda }=\frac{1}{{\displaystyle {\sum }_i^n\frac{1}{{\bar{\lambda }}_i}}}$ (6)

This way to find the Compton wavelength of a composite particle is fully consistent with aggregating masses in the standard way:

$m={\displaystyle \underset{i}{\overset{n}{\sum }}}{m}_i$ (7)

The formula above is strictly only valid for non-bound masses. For bound masses, the mass is typically slightly lower than the mass aggregates of its individual components due to the release of binding energy [48] . This can easily be adjusted for, as energy can be treated as mass equivalent from Einstein’s principle of $m=\frac{E}{c^2}$ .

If we know the Planck constant and the kilogram mass of any mass in question, even the kilogram mass of large objects like, for example, the Earth or the sun, then we can easily find its reduced Compton wavelength. It is simply given by $\bar{\lambda }=\frac{\hslash }{mc}$ . For masses larger than the Planck mass, the reduced Compton wavelength will be shorter than the Planck length. No physical Compton wavelength can likely be shorter than the Planck length, but the aggregates of Compton wavelengths that are all larger than the Planck length can be shorter than the Planck length. This is related to the fact that the aggregated Compton wavelength is given by Formula (6).

However, to find the kilogram mass of the Earth or the sun, we typically need to know G. Later on, we will need to find the Compton wavelength of larger masses without knowing G and also without knowing ħ. This is fully possible. First, one can find the Compton wavelength from an electron, as it also can be described by the following Formula (see [35] [42] ):

$\lambda =\frac{{\lambda }_{1,\gamma }-{\lambda }_{2,\gamma }}{1-\cos \theta }$ (8)

where $\theta$ is the angle between the ingoing and outgoing photon from photon scattering. Further, ${\lambda }_{\mathrm{1,}\gamma }$ and ${\lambda }_{\mathrm{2,}\gamma }$ are the wavelength of the photon when sent towards the electron and when reflected from the electron. All these are measurable without knowledge off ħ or G.

Next, we can find the Compton wavelength by utilizing cyclotron frequencies. The cyclotron frequency is given by:

$f=\frac{qB}{m2\pi }$ (9)

and since electrons and protons have the same absolute value of the charge, $\left|q\right|$ , then the cyclotron frequency ratio of electrons and protons are proportional to their mass ratio. That is, we must have:

$\frac{m_p}{m_e}=\frac{f_e}{f_P}=\frac{\frac{qB}{m_{P}2\pi }}{\frac{qB}{m_{e}2\pi }}=\frac{{\bar{\lambda }}_e}{{\bar{\lambda }}_P}$ (10)

So, when we have measured the cyclotron frequency of electrons and protons, we can find the proton electron mass ratio (without knowing ħ). It has experimentally been found to be approximately 1836.15 by indeed using the cyclotron method; see [49] [50] [51] . All we now need in order to find the Compton wavelength of the proton is to divide the Compton wavelength of the electron by the cyclotron ratio of 1836.15. For any larger masses, one will now get a very accurate approximation of the Compton wavelength of that mass by counting the number of protons in it and dividing by that number. For simplicity, we do not need to distinguish between neutrons and protons as they have almost the same mass, or we can do the small mass adjustment. This method will lead to the estimated Compton wavelength being off by less than one percent. The up to 1% error is because we have not considered binding energy. However, we can also easily estimate the binding energy and adjust for it. However, for our purpose that we will come to later, we can do well enough without even adjusting for binding energy.

To count the number of atoms in a mass is, however, not trivial. For macroscopic masses that we can hold in our hand, it is however practically possible. Actually, one of the competing methods for the 2019 redefinition of the kilogram mass consisted of counting very accurately the number of atoms in silicon spheres; see [52] [53] [54] [55] . Silicon crystals have a very uniform structure (²⁸Si), so by counting a few of them and knowing the volume of, for example, a silicon sphere very accurately, one can easily estimate the number of atoms in it.

Still, what about large masses like the Earth or the sun? Also, here we can easily find the Compton wavelength as we must have the following relation:

$\frac{g_1{R}_1^2}{g_2{R}_2^2}=\frac{{\bar{\lambda }}_2}{{\bar{\lambda }}_1}$ (11)

So, we can easily find the gravitational acceleration of a small silicon sphere that we have counted the number of atoms in and therefore also know the Compton wavelength of; this we can do in a Cavendish apparatus. Some will possibly think that if we use a Cavendish apparatus then we need to know G, but this is not the case. Actually, Cavendish himself never used nor suggested a gravitational constant when he measured the density of the Earth; see [56] . The gravitational acceleration in the Cavendish apparatus is given by:

$g=\frac{L4{\pi }^2{\theta }_c}{T^2}$ (12)

where L is the length of the arm between center to center of the two small balls in the apparatus. Further, ${\theta }_c$ is the angle of deflection of the arm and T is the measured oscillation period. Clearly no G or ħ are needed to measure this also. Next, to find the gravitational acceleration field of the Earth, for example, one can simply drop a ball from height H to the ground. The gravitational acceleration is then given by $g=\frac{2H}{T^2}$ where T is the time it took for the ball to fall to the ground. We now have all we need to also calculate the Compton wavelength of large objects like the Earth, independent of G or ħ.

In the next section we will see how the Compton wavelength plays a critical role in finding the Planck time from simple gravitational measurements.

4. Measuring the Planck Time Independent of Knowledge of G, c and h

To find the Planck length without knowledge of G or h or c, we can measure the gravitational bending of light, for example from the sun, and the gravitational acceleration, for example from the Earth. That is, we need to combine two gravitational measurements. These two gravitational measurements can be from the same object, for example both from the sun, or they can be from two different objects, for example the sun and the Earth, something that is more practical. The general formula for the Planck time is then given by (as first presented here):

$t_p=\frac{\delta }{4\sqrt{g}}\frac{R_1{\bar{\lambda }}_1}{R_2\sqrt{{\bar{\lambda }}_2}}$ (13)

where $\delta$ is the measured light bending at radius R₁ from the gravitational object, g is the measured gravitational acceleration from the other gravitational object at radius $R_2$ , and ${\bar{\lambda }}_1$ and ${\bar{\lambda }}_2$ are the reduced Compton wavelength of, respectively, the mass affecting the gravitational deflection of light and the mass we measure the gravitational acceleration from. We will get back to how to derive it in the next section.

Let’s take a numerical example. The gravitational acceleration we can measure on the surface of the Earth; it is approximately 9.84 m/s². Be aware that to measure it we need no knowledge of G or ħ. We can, for example, measure it by simply dropping a ball from height H above the ground and simply measuring the time it takes from when we dropped it until it hits the ground. The gravitational acceleration is then given by $g=\frac{2H}{T^2}$ . It is only when we want to predict the gravitational acceleration from Newton or general relativity theory that we need to know G, not to measure it. In the Planck time Equation (13) above, we need the radius of the Earth; this is approximately $R_2=6371000$ meters. The deflection of a light beam passing the sun has been measured to be approximately 1.75 arcseconds. This corresponds to approximately 85 × 10⁻⁷ radians. The radius of the sun is approximately $R_1=696340000$ meters. The reduced Compton wavelength of the sun and the Earth are respectively 1.77 × 10⁻⁷³ m and 5.89 × 10⁻⁶⁸ m. Inputting this in Equation (13) gives:

$t_p=\frac{85\times {10}^{-7}}{4\sqrt{9.84}}\frac{696340000\times 1.77\times {10}^{-73}}{6371000\sqrt{5.89\times {10}^{-68}}}\approx 5.4\times {10}^{-44}\text{s}$

This is the Planck time found without any knowledge of G, h, and c. Or actually, it can be discussed if we need to know c when finding the Compton wavelength, but we definitely do not need any knowledge of G or the Planck constant.

In the special case where the gravitational acceleration is measured from the same gravitational object and the same mass as the light bending, then Equation (13) can be simplified to:

$t_p=\frac{\delta \sqrt{\bar{\lambda }}}{4\sqrt{g}}$ (14)

Alternatively, for gravitational acceleration we could, for example, have used orbital velocity to find the Planck time. Then we have the following relation:

$t_p=\frac{\delta }{4v_o}\frac{R_1{\bar{\lambda }}_1}{\sqrt{R_2{\bar{\lambda }}_2}}$ (15)

That is, again to find the Planck time independently of G, ħ, and c, we need to do two gravitational measurements: the bending of light and the orbital velocity. Or we can find the Planck time from only one gravitational measurement if we know the speed of light. The Planck time is equal to:

$t_p=\frac{R\sqrt{g\bar{\lambda }}}{c^2}$ (16)

where R is the distance from the center of the gravitational object to where the measurements of the gravitational acceleration g take place.

The breakthrough in understanding that we can measure any Planck units without knowledge of G or h basically came with the understanding that matter ticks at the reduced Compton frequency and then the reduced Compton wavelength is the true matter wavelength, while the de Broglie wavelength [38] [39] is only a mathematical derivative of the Compton wavelength.

Table 1 shows a series of ways to find the Planck time with no knowledge of G or ħ, and some ways to find it without knowledge of G, ħ, and c. To find the Planck time from a pendulum clock has recently been described in [57] and from a Cavendish apparatus in [37] , but the other methods are basically described for the first time here.

5. How Did We Come Up with These Formulas?

Anyone can input values in the formulas above from experiments and test that what comes out is the Planck time. Still, how did we come up with these formulas? Do they have a proper foundation? Anyone can ad hoc put together some crackpot formulas by trial and error and get some output similar to the value of the Planck length; that would be numerology. It is hard to see from the formulas how we got to them. The way we got to them is, however, rooted in a solid foundation and deep understanding of the Planck scale and other quantum aspects of matter and gravity. One of the keys is the Compton wavelength formula. It is given by:

$\lambda =\frac{h}{mc}$ (17)

The key is to solve this with respect to m, and this gives:

$m=\frac{h}{\lambda }\frac{1}{c}=\frac{\hslash }{\bar{\lambda }}\frac{1}{c}$ (18)

The second insight is that we can solve the Planck length formula for G, and this gives $G=\frac{l_p^2{c}^3}{\hslash }$ . In all observable gravitational phenomena, we have GM and not GMm, as discussed in [58] . This means ħ always cancels out, as it is not needed for gravity. Further, by now using the conventional formulas, for example for gravitational deflection, $\delta =\frac{4GM}{c^{2}R}=\frac{4l_p^2}{\bar{\lambda }R}$ and gravitational acceleration, $g=\frac{c^2{l}_p^2}{R^2\bar{\lambda }}$ we can now see that we can combine these to get $t_p=\frac{l_p}{c}$ . If we take the gravitational deflection and divide it by the square root of the gravitational acceleration, we can see we get:

Table 1. The table shows various ways we can find the Planck time without knowledge of G, h, and c, as well as without knowledge of G and h.

$\frac{\delta }{\sqrt{g}}=\frac{\frac{4l_p^2}{\bar{\lambda }R}}{\sqrt{\frac{c^2{l}_p^2}{R^2\bar{\lambda }}}}=\frac{4l_p}{c\sqrt{\bar{\lambda }}}$ (19)

In other words, this must be multiplied by $\bar{\lambda }$ and divided by four to be left with only the Planck time, $t_p=\frac{l_p}{c}$ , so we end up with:

$t_p=\frac{\delta \sqrt{\bar{\lambda }}}{4\sqrt{g}}$

which is our equation number (14).

Similarly, all the other formulas can be simply derived. We can ensure all the formulas given above are not just some approximation or randomly put together formulas, but they are exact and it is suddenly possible to easily find the Planck time and other aspects of the Planck scale from a few gravitational observations and without any knowledge of G. This because we now understand both G and m from a deeper perspective. The Newton gravitational constant, which actually was first invented in 1873 by Cornu and Baily [59] ¹ is, in reality, a composite constant (see [61] ) and the matter wavelength is the Compton wavelength. When combining these simple insights, it is easy to detect the Planck scale. This again has led us to a recent quantum gravity theory.

We can even build up a full quantum gravitational theory without relying on G or h; this has recently been done [27] [44] , but it is naturally up to others to scrutinize and investigate.

6. The Hidden Quantization in Gravity

In standard physics, we have quantization of energy linked to the Planck constant h as pure electromagnetic energy can be described as $E=h\frac{c}{{\lambda }_{\gamma }}$ . In gravity, we do not need the Planck constant to get quantization.

The hidden Planck constant in the mass and in G always cancel each other out, as we, in “all” observable gravitational phenomena, have:

$GM=\frac{l_p^2{c}^3}{\hslash }\times \frac{\hslash }{\bar{\lambda }}\frac{1}{c}=c^3\frac{l_p}{c}\frac{l_p}{\bar{\lambda }}=c^3{t}_p\frac{l_p}{\bar{\lambda }}$ (20)

Therefore, there are no Planck constants needed to predict any gravitational phenomena, as it always cancels out. Still, it is expected that a final gravitational quantum theory will have quantization of gravity. To our own surprise, the quantization is already hidden in standard gravity if one just digs deep enough. That is, when one expresses G as a composite constant and M as $M=\frac{\hslash }{\lambda }\frac{1}{c}$ and calculates out the various gravitational formals, then GM can be seen as a way to turn the incomplete kilogram mass, which is a human arbitrarily chosen unit, and construct a more complete mass, namely $M_g=\frac{l_p}{c}\frac{l_p}{\bar{\lambda }}=t_p\frac{l_p}{\bar{\lambda }}$ . This new mass definition can also be found by simply taking $\frac{GM}{c^3}$ , so it is basically already embedded in standard gravitational physics. It is just that G was inserted ad hoc in 1873, and was never derived from deeper principles, and has therefore not been understood until recently. The gravitational constant is found, from calibration, to fix the incomplete kilogram mass so the gravitational formulas can be used to accurately predict gravitational phenomena. The gravitational constant, by calibration to gravity phenomena, is able to capture what is missing in the incomplete kilogram mass.

Pay attention to the fact that our new mass definition (collision-time mass) that is embedded (and concealed) in standard gravitational theory, it is given by:

$\frac{G}{c^3}M=M_g=\frac{l_p}{c}\frac{l_p}{\bar{\lambda }}=t_p\frac{l_p}{\bar{\lambda }}=t_p{n}_p$ (21)

This mass² is simply equal to the Planck time multiplied by $\frac{l_p}{\bar{\lambda }}$ . This last part $\frac{l_p}{\bar{\lambda }}$ corresponds to the number of Planck mass events, $n_p$ , in the gravitational mass $M_g$ per Planck time. This is discussed in detail in a new unified quantum gravity theory that is rooted in the Planck scale and an indivisible time interval; see [26] [27] [44] . And as we have clearly demonstrated in the previous section, there is no need to know G or ħ to find the Planck time, so we can also find this collision-time mass directly without knowledge of such constants. In other words, we do not need to know G and multiply it with M to find this new mass, as we have also demonstrated in other papers.

For a Planck mass, this last term $\frac{l_p}{\bar{\lambda }}$ is one. So, in a Planck mass particle there is one Planck mass event per Planck time, and its duration is only the Planck time. For a mass smaller than the Planck mass, it is less than one; that is, it is then the probability for a Planck mass event to happen in the observational time interval of the Planck time. For large macroscopic masses, this factor will be an integer plus a small fraction. The integer part then represents the number of Planck events per Planck time happening in that mass, and the remaining fraction part is the probability for one more such event. For the sun, we have that this factor is approximately $\frac{l_p}{\bar{\lambda }}\approx 9.15\times {10}^{37}$ events per Planck time. That is, the gravity is quantized. So, what we actually measure is the enormous amount of Planck times aggregated, but we are able to separate them and even find the one Planck time as matter can be seen as clocks ticking at the Compton frequency. However, this clocks have two properties. The time between each Planck event is the Compton time, that is $\frac{\bar{\lambda }}{c}$ while the Planck event itself lasts the Planck time. You can think of it is as a clock that every hour says: Ding. The Compton time is the time between each ding, but what is the duration of the ding itself? That is the Planck time, and it is the ding itself that is a Planck mass event that is the cause of gravity; see [26] [27] [44] . See the papers just referred to for an in-depth discussion and for a suggestion for a unified quantum gravity theory.

Table 2 shows how to find the number of Planck events inside the gravitational mass per Planck time.

Table 2. The table shows various ways we can find the number of Planck mass events $\frac{l_p}{\bar{\lambda }}$ without knowledge of G, h, and c as well as without knowledge of G and h.

Table 2 above gives the number of Planck events per Planck time; that is, for the indivisible time interval. We can easily convert all the formulas above to the arbitrarily human chosen time interval of one second by multiplying all formulas in Table 2 with: $\frac{1}{t_p}$ . One then end up with $\frac{c}{\bar{\lambda }}=f_c$ , in other words, the reduced Compton frequency per second, which again is the number of Planck events per second in the gravitational mass.

7. The Number of Planck Mass Events in a Planck Mass Particle

Interesting is the special case of the Planck mass particle when we are at a distance equal to the Planck length. For example the Planck acceleration is then $a_p=\frac{c^2}{l_p}$ , and the number of Planck mass events as predicted from this is given by the formula in the table, it is:

$\frac{l_p}{\bar{\lambda }}=n_p=\frac{R\sqrt{g}}{c\sqrt{\bar{\lambda }}}=\frac{l_p\sqrt{\frac{c^2}{l_p}}}{c\sqrt{l_p}}=1$ (22)

That is the Planck mass particle is a Planck mass event that last the Planck time as has been suggested not only by asumption, but by calibration in a new quantum gravity theory, see [26] [27] . The same answer one get from the orbital velocity formula, for a Planck mass particle the orbital velocity is $v_0=c$ and it gives

$\frac{l_p}{\bar{\lambda }}=n_p=\frac{v_0\sqrt{R}}{c\sqrt{\bar{\lambda }}}=\frac{c\sqrt{l_p}}{c\sqrt{l_p}}=1$ (23)

This means if one observe a Planck mass particle in the Planck time then it is always in a collision state. The Planck mass is in a new quantum gravity theory [27] simply the collision between two photons (light particles). Also in standard theory mass can be created from photon photon collisions.

8. Consistent with a New Quantum Version of General Relativity Theory

We have demonstrated above how one can extract the number of Planck mass events in any gravitational mass, even the Hubble sphere. This is consistent with a new approach to quantizing the general relativity theory. Einstein’s [62] field equation is given by:

$R_{\mu \nu }-\frac{1}{2}R{g}_{\mu \nu }=\frac{8\pi G}{c^4}{T}_{\mu \nu }.$ (24)

However, when we solve the Max Planck formula for the Planck length for G, we obtain $G=\frac{l_p^2{c}^3}{\hslash }$ , and replacing G with this in Einstein’s field equation gives (see [63] [64] ):

$R_{\mu \nu }-\frac{1}{2}R{g}_{\mu \nu }=\frac{8\pi t_p{l}_p}{\hslash }{T}_{\mu \nu }.$ (25)

This only makes sense if one can find the Planck length or Planck time independent of G, something that has been demonstrated to be fully possible in recent years and also in this paper. Furthermore, for example, the Schwarzschild metric can then be written as:

$\text{d}{s}^2=-\left(1-\frac{2l_p}{r}\frac{l_p}{{\bar{\lambda }}_M}\right)c^2\text{d}{t}^2+{\left(1-\frac{2l_p}{r}\frac{l_p}{{\bar{\lambda }}_M}\right)}^{-1}\text{d}{r}^2+r^2\text{d}{\Omega }^2$ (26)

where $\text{d}{\Omega }^2=\text{d}{\theta }^2+{\sin }^2\theta \text{d}{\varphi }^2$ and ${\bar{\lambda }}_M$ represents the reduced Compton wavelength of the gravitational mass M. The term $\frac{l_p}{{\bar{\lambda }}_M}$ denotes the reduced Compton frequency per Planck time, and in Section 7, we have demonstrated how this can be extracted from gravitational observations without any knowledge of G. This is what makes this version of general relativity quantized. The gravitational mass M has a number of Planck mass events per Planck time equal to $\frac{l_p}{{\bar{\lambda }}_M}$ . If the mass is equal to the Planck mass, then $\frac{l_p}{{\bar{\lambda }}_M}=\frac{l_p}{l_p}=1$ . For masses smaller than the Planck mass, the frequency per Planck time is below one. As the lowest observable frequency is one, this should, in our view, be interpreted as the frequency probability of a Planck mass hit. Therefore, gravity for a mass below the Planck mass is probabilistic. For macroscopic objects from Planck mass size and much larger, gravity is, on the other hand, deterministic.

As Haug [65] has recently also demonstrated, we have: $\frac{T_{\text{cmb}}^2}{T_{\text{Haw}}^2}=\frac{l_p}{\bar{\lambda }}$ when we work with black holes. This is based on the assumption that the temperature inside the black hole is

$T_{\text{cmb}}=\frac{\hslash c}{k_{b}4\pi \sqrt{R_{s}2l_p}}$ (27)

where $R_s=\frac{2GM}{c^2}$ , which is the Schwarzschild radius of the black hole. This formula was basically first presented by Tatum et al. [66] and has later been demonstrated to be derived from the Stefan-Boltzmann law by Haug and Wojnow [65] [67] , as well as by Haug and Tatum [68] through a geometric mean approach.

The Schwarzschild metric can therefore even be written in what we can call a thermodynamic form that is valid for all black holes:

$\text{d}{s}^2=-\left(1-\frac{2l_p}{r}\frac{T_{\text{cmb}}^2}{T_{\text{Haw}}^2}\right)c^2\text{d}{t}^2+{\left(1-\frac{2l_p}{r}\frac{T_{\text{cmb}}^2}{T_{\text{Haw}}^2}\right)}^{-1}\text{d}{r}^2+r^2\text{d}{\Omega }^2$ (28)

That is, there is a strong thermodynamic connection to black holes as initially investigated by Bekenstein and Hawking, but now even incorporated in the Schwarzschild metric itself. So this means $\frac{T_{\text{cmb}}^2}{T_{\text{Haw}}^2}$ is also directly linked to the Planck time as this is the reduced Compton frequency per Planck time in the mass of the black hole.

9. Can We Really Detect the Planck Time?

Can we truly detect the Planck time or the Planck length? The Planck time is significantly shorter than what even the most advanced optical clocks can measure, which is about 10⁻¹⁹ seconds, see [69] [70] [71] [72] . Currently, and likely in the future, we cannot measure a single Planck time. However, if we assume that the Compton frequency is the true cause of quantization in matter (and gravity), then at each Compton time interval, a Planck mass event occurs, at least according to recent theories in collision-time quantum gravity theory (see [27] ) as well as in a recent quantum version of general relativity theory, see [65] [73] . Thus, what we are capable of measuring is a large aggregate of these Planck mass events, each lasting for the Planck time. Such massive aggregates of events are only found in macroscopic masses. Additionally, since we can also identify the reduced Compton frequency in the gravitational object of interest, for example, a one-kilogram ball used in a Cavendish apparatus, we can then isolate the Planck time. This mean the Planck time is discovered, not only theoretically, but physically. That idea that there was a indivisible time interval, that strangely enough was first described directly in the New testament, and later by Isaac Newton has now been discovered, it is the Planck time and it is fully measurable and has recently led to even a new quantized form of general relativity theory.

10. Planck Time (God Time) from Cosmology

The Planck time can also be derived from the Cosmic Microwave Background (CMB) temperature combined with the cosmological red-shift and the Hubble constant. The Planck time is given by

$t_p=\frac{H_0}{T_{CMB}^2}\frac{{\hslash }^2}{k_b^{2}32{\pi }^2}\approx 5.39\times {10}^{-44}\text{s}$ (29)

when using a Hubble constant of 66.8 km/s/Mpc (2.167 × 10⁻¹⁸) s⁻¹ and a CMB temperature of 2.725 K, see [74] [75] [76] [77] . To understand how we arrive at this formula, we must refer to [65] . Alternatively, from the cosmological red-shift and CMB temperature, the formula is:

$t_p=\frac{z}{d{T}_{CMB}^2}\frac{{\hslash }^{2}c}{k_b^{2}32{\pi }^2}\approx 5.39\times {10}^{-44}\text{s}$ (30)

where d represents the distance to the emitted photons, and z is the cosmological red-shift.

Furthermore, the reduced Compton time for the critical Friedmann mass in the Hubble sphere is given by:

$t_c=\frac{\bar{\lambda }c}{c}=\frac{H_0^3}{T_{CMB}^4}\frac{{\hslash }^4}{k_b^{4}512{\pi }^4}\approx 1.26\times {10}^{-104}\text{s}$ (31)

This is much shorter than the Planck time, indicating that many events occur within one Planck time inside the Hubble sphere, each with a duration of the Planck time.

Furthermore, the reduced Compton frequency per Planck time, $n_p=\frac{l_p}{{\bar{\lambda }}_c}$ , for the critical mass in the Hubble sphere is:

$n_p=\frac{l_p}{{\bar{\lambda }}_c}=\frac{T_{CMB}^2}{H_0^2}\frac{k_b^{2}16{\pi }^2}{{\hslash }^2}\approx 4.28\times {10}^{60}\text{frequency}\text{per}\text{Planck}\text{time}$ (32)

This represents the number of bits computed by the Hubble sphere per Planck time. In this context, the Hubble sphere can be seen as the most powerful computer, metaphorically referred to as the “God Computer.” It calculates an astonishing 7.93 × 10¹⁰³ bits per second. The fastest human-made computer at the time of writing only performs about 1 quintillion operations per second, which is like nothing compared to this.

11. The Hubble Time, the Planck Time, the Compton Time and the Holy Trinity of Space-Time

The Hubble constant, first introduced and estimated by Lemaître and Hubble, has recently been understood from a deeper quantum perspective. The Hubble time (the assumed age of the universe) is simply given by $t_h=\frac{1}{H_0}$ . The Hubble time is the longest time in cosmos we know about that we can indirectly estimate and is relevant to the universe we live in. The Planck time is the shortest time, it is the indivisible time intervale. Here we will demonstrate there is a direct relation between the two. In the critical Friedmann [78] universe, the Hubble constant can be described as (see [79] [80] ):

$H_0=\frac{1}{2t_p\frac{l_p}{{\bar{\lambda }}_c}}$ (33)

where ${\bar{\lambda }}_c$ is the reduced Compton wavelength of the critical Friedmann mass, and as before, $\frac{l_p}{{\bar{\lambda }}_c}$ is the reduced Compton frequency per Planck time. Furthermore, the Hubble time must then be given by:

$t_h=\frac{1}{H_0}=2t_p\frac{l_p}{{\bar{\lambda }}_c}$ (34)

This means the Planck time can also be extracted from the Hubble constant; it is given by:

$t_p=\sqrt{\frac{{\bar{\lambda }}_c}{H_{0}2c}}=\sqrt{t_h\frac{{\bar{\lambda }}_c}{2c}}=\sqrt{t_h\frac{1}{2}{t}_c}$ (35)

where $t_h$ is the Hubble time, and $t_c$ is the reduced Compton time of the critical Friedmann universe. This result was indirectly shown by Haug, who provided the formula: $l_p=\sqrt{\frac{1}{2}{R}_s\bar{\lambda }}$ , in 2018. Additionally, since the Hubble radius is identical to the Schwarzschild radius: $R_s$ , in the critical Friedman universe, one can derive Equation (35) from this equation simply by dividing it by c.

In the extremal universe [81] that emerges from the extremal solution of the Reissner-Nordström [82] [83] , Kerr [84] , and Kerr-Newman [85] metrics, as well as in the Haug and Spavieri [86] [87] universe, we must have:

$H_0=\frac{1}{t_p\frac{l_p}{{\bar{\lambda }}_u}}$ (36)

where ${\bar{\lambda }}_u$ is the reduced Compton wavelength of the mass in the extremal universe or the Haug-Spavieri universe. This mass (mass equivalent) is exactly twice the mass in the critical Friedmann universe: $2M_c=\frac{c^3}{G{H}_0}$ . Furthermore, we have that the Hubble time is given by:

$t_h=\frac{t_p^2}{t_c}$ (37)

So, in the extremal universe or in the Haug-Spavieri universe, we have:

$t_p=\sqrt{\frac{{\bar{\lambda }}_u}{H_{0}c}}=\sqrt{\frac{t_h{\bar{\lambda }}_u}{c}}=\sqrt{t_h{t}_c}$ (38)

where $t_h$ is the Hubble time and $t_c$ is the reduced Compton time in the extremal universe as well as in the Haug-Spavieri cosmological model. This means the Planck time is the geometric mean time of the Hubble time and the reduced Compton time of the universe.

Table 3 summarizes direct relationships between microcosmos and cosmos in the form of direct relations between the Planck time, the Hubble time, and the

Table 3. This table summarize the direct relations between the Planck time, the Hubble time and the reduced Compton time.

Figure 1. This figure shows the relationship between Planck time (the indivisible time interval), the Hubble time and the reduced Compton time.

reduced Compton time, as well as for the Planck length, the Hubble radius, and the reduced Compton wavelength.

Figure 1 summarizes the relationship between the Planck time, the Hubble time, and the reduced Compton time, as well as the relationship between the Planck length, the Hubble radius, and the reduced Compton wavelength of the extremal universe or the Haug-Spavieri cosmological model.

12. Conclusion

We have looked at the history of the indivisible time interval. An indivisible time interval was mentioned in the New Testament, something that seems to have got lost in modern English translations. Isaac Newton clearly mentioned an indivisible time interval in his book Principia, though it is unclear if he got the idea for this from the New Testament and it is also not important. Today, the Planck time is considered by many physicists to be the smallest possible time interval and therefore somehow indivisible. However, very recently one has been able for the first time to measure the Planck time without calculating it from dimensional analysis. The Planck time can be found by combining two gravitational observations without any knowledge off G, ħ, and c, or just from one gravitational observation if one only wants it independent of G and ħ. This strongly supports the recent view that to observe simple effects from gravity itself, such as gravitational acceleration or orbital velocity, is remarkably a detection of the Planck scale. This is also in line with a recent quantum gravity theory that claims to unify gravity with quantum mechanics. If this attempt will be considered a useful one or not, only time will tell, when more researchers have carefully investigated it.

NOTES

¹They used the notation f for the gravity constant, while Boys [60] in 1894 is likely the first to use the notation G.

²In some previous papers we have used symbol notation $\bar{M}$ for what we here use symbol $M_g$ for.

Conflicts of Interest

The author declares no conflict of interest.

References

[1]	Lederman, L. (1993) The God Particle. Dell Publishing, New York.
[2]	Newton, I. (1686) Philosophiae Naturalis Principia Mathematica. Jussu Societatis Regiae ac Typis Josephi Streater, London. https://doi.org/10.5479/sil.52126.39088015628399
[3]	Heberle-Bors, E. (2004) Bible Study Led Newton to Scientific Discoveries. Nature, 432, 271. https://doi.org/10.1038/432271c
[4]	Taylor, C.C.W. (1999) The Atomists: Leucippus and Democritus, Fragments and Translation with Commentary. University of Toronto Press, Toronto.
[5]	Guthrie, W.K.C. (1962) A History of Greek Philopsophy, the Earlier Presocratics and the Pythagoreans. Cambridge University Press, Cambridge.
[6]	Bonner, G., et al. (1995) Sermons: The Work of Saint Augustine, a Translation for the 21 Century: “Explaining the Atom of and the Twinkling of an Eye in Which the Dead Are All Going to Rise Again” Sermon Number 362, Page 256. New City Press, New York.
[7]	MacCarron, M. (2021) Bede and Time, Computus, Theology and History in the Early Medieval World. Routledge, New York.
[8]	Doyle, C. (2021) Atoms and Time I. In: Zilioli, U., Ed., Atomism in Philosophy, Bloomsbury Publishing, New York, 216-223. https://doi.org/10.5040/9781350107526.0019
[9]	Redondi, P. (1989) Galileo: Heretic. Princeton University Press, Princeton. https://doi.org/10.1063/1.2810883
[10]	Lemaître, G. (1927) Un univers homogétne de masse constante et de rayon croissant rendant compte de la vitesse radiale des nétbuleuses extra-galactiques. Annales de la Sociétét Scientifique de Bruxelles, 47, 49-56.
[11]	Hubble, E. (1926) Extragalactic Nebulae. Astrophysical Journal, 64, 321-369. https://doi.org/10.1086/143018
[12]	Williams, H.S. and Williams, E.H. (1904) A History of Science. Harper and Brothers, New York. https://doi.org/10.5962/bhl.title.21282
[13]	Gæury, M. (2013) Epicurean Time Atomism and Aristotle’s Physics. Les Etudes Philosophiques, 107, 535-552. https://www.cairn.info/revue-les-etudes-philosophiques-2013-4-page-535.htm
[14]	Maimonides, M. (1190) A Guide for the Perplexed.
[15]	Planck, M. (1899) Natuerliche Masseinheiten. Der Königlich Preussischen Akademie Der Wissenschaften, Berlin. https://www.biodiversitylibrary.org/item/93034#page/7/mode/1up
[16]	Planck, M. (1906) Vorlesungen über die Theorie der Wärmestrahlung. J.A. Barth, Leipzig, 163.
[17]	Wadlinger, R.L. and Hunter, G. (1988) Max Planck’s Natural Units. The Physics Teacher, 26, 528-529. https://doi.org/10.1119/1.2342611
[18]	Ng, Y.J., Christiansen, W.A. and van Dam, H. (2003) Probing Planck-Scale Physics with Extragalactic Sources? The Astrophysical Journal, 591, L87. https://doi.org/10.1086/377121
[19]	Gharibyan, V. (2012) Testing Planck-Scale Gravity with Accelerators. Physical Review Letters, 1090, Article ID: 141103. https://doi.org/10.1103/PhysRevLett.109.141103
[20]	Hees, A., et al. (2017) Tests of Lorentz Symmetry in the Gravitational Sector. Universe, 2, Article No. 30. https://doi.org/10.3390/universe2040030
[21]	Zanon-Willette, T., Lefevre, R., Sillitoe, R.M. and Almonacil, N.S. (2018) Composite Laser-Pulses Spectroscopy for High-Accuracy Optical Clocks: A Review of Recent Progress and Perspectives. Reports on Progress in Physics, 81, Article ID: 094401. https://doi.org/10.1088/1361-6633/aac9e9
[22]	Wendel, G., Martínez, L. and Bojowald, M. (2020) Physical Implications of a Fundamental Period of Time. Physical Review Letters, 124, Article ID: 241301. https://doi.org/10.1103/PhysRevLett.124.241301
[23]	Adler, S.L. (2010) Six Easy Roads to the Planck Scale. American Journal of Physics, 78, 925-932. https://doi.org/10.1119/1.3439650
[24]	Hossenfelder, S. (2012) Can We Measure Structures to a Precision Better than the Planck Length? Classical and Quantum Gravity, 29, Article ID: 115011. https://doi.org/10.1088/0264-9381/29/11/115011
[25]	Ball, P. (1999) Physics at the Planck Time. Nature, 402, C61. https://doi.org/10.1038/35011550
[26]	Haug, E.G. (2020) Collision Space-Time: Unified Quantum Gravity. Physics Essays, 330, 46-78. https://doi.org/10.4006/0836-1398-33.1.46
[27]	Haug, E.G. (2022) Unified Quantum Gravity Field Equation Describing the Universe from the Smallest to the Cosmological Scales. Physics Essays, 35, 61-71. https://doi.org/10.4006/0836-1398-35.1.61
[28]	Cohen, E.R. (1987) Fundamental Physical Constants. In: Sabbata and Melniko, V.N., Eds., Gravitational Measurements, Fundamental Metrology and Constants, Kluwer Academic Publishers, Amsterdam, 59. https://doi.org/10.1007/978-94-009-2955-5_5
[29]	McCulloch, M.E. (2016) Quantised Inertia from Relativity and the Uncertainty Principle. Europhysics Letters (EPL), 1150, Article No. 69001. https://doi.org/10.1209/0295-5075/115/69001
[30]	Strehl, K. (1913) Raum-und Zeitaome. Das Weltall, 13, 333. https://www.astw.de/publikationen/weltall/pdf/weltall_jg_13.pdf
[31]	Eddington, A.S. (1918) Report on the Relativity Theory of Gravitation. The Physical Society of London, Fleetway Press, London.
[32]	Bridgman, P.W. (1931) Dimensional Analysis. Yale University Press, New Haven.
[33]	Das, S. and Modak, S.K. (2021) A Novel Mechanism for Probing the Planck Scale. Classical and Quantum Gravity, 39, Article ID: 015005. https://doi.org/10.1088/1361-6382/ac38d3
[34]	Haug, E.G. (2017) Can the Planck Length Be Found Independent of Big G? Applied Physics Research, 9, 58-66. https://doi.org/10.5539/apr.v9n6p58
[35]	Haug, E.G. (2020) Finding the Planck Length Multiplied by the Speed of Light without Any Knowledge of G, C, or H, Using a Newton Force Spring. Journal Physics Communication, 4, Article ID: 075001. https://doi.org/10.1088/2399-6528/ab9dd7
[36]	Haug, E.G. (2021) Measurements of the Planck Length from a Ball-Clock without Knowledge of Newton’s Gravitational Constant G or the Planck Constant. European Journal of Applied Physics, 3, 15-20. https://www.ej-physics.org/index.php/ejphysics/article/view/133
[37]	Haug, E.G. (2022) Planck Units Measured Totally Independently of Big G. Open Journal of Microphysics, 12, 55-85. https://doi.org/10.4236/ojm.2022.122004
[38]	de Broglie, L. (1924) Recherches sur la théorie des quanta. Annalen der Physik, 10, 22-128. https://doi.org/10.1051/anphys/192510030022
[39]	de Broglie, L. (1930) An Introduction to the Study of Wave Mechanics. Metheum & Co., Essex.
[40]	Davisson, C. and Germer, L.H. (1927) Diffraction of Electrons by a Crystal of Nickel. Physical Review, 300, 705-741. https://doi.org/10.1103/PhysRev.30.705
[41]	Compton, A.H. (1923) A Quantum Theory of the Scattering of X-Rays by Light Elements. Physical Review, 210, 483-502. https://doi.org/10.1103/PhysRev.21.483
[42]	Haug, E.G. (2022) Derivation of a Relativistic Compton Wave. European Journal of Applied Physics, 4, 24-27. https://doi.org/10.24018/ejphysics.2022.4.4.190
[43]	Haug, E.G. (2020) Rethinking the Foundation of Physics and Its Relation to Quantum Gravity and Quantum Probabilities: Unification of Gravity and Quantum Mechanics. https://www.preprints.org/manuscript/202012.0483/v2
[44]	Haug, E.G. (2021) Quantum Gravity Hidden in Newton Gravity and How to Unify It with Quantum Mechanics. In: Krasnoholovets, V., Ed., The Origin of Gravity from the First Principles, NOVA Publishing, New York, 133-216.
[45]	Haug, E.G. (2018) Newton and Einstein’s Gravity in a New Perspective for Planck Masses and Smaller Sized Objects. International Journal of Astronomy and Astrophysics, 8, 6-23. https://doi.org/10.4236/ijaa.2018.81002
[46]	Levitt, L.S. (1958) The Proton Compton Wavelength as the “Quantum” of Length. Experientia, 14, 233-234. https://doi.org/10.1007/BF02159173
[47]	Trinhammer, O.L. and Bohr, H.G. (2019) On Proton Charge Radius Definition. EPL, 128, Article No. 21001. https://doi.org/10.1209/0295-5075/128/21001
[48]	D’Auria, S. (2018) Introduction to Nuclear and Particle Physics. Springer, Berlin.
[49]	Sturm, S., et al. (2014) High-Precision Measurement of the Atomic Mass of the Electron. Nature, 506, 467. https://link.springer.com/article/10.1007/BF01414243
[50]	Gräff, G., Kalinowsky, H. and Traut, J. (1980) A Direct Determination of the Proton Electron Mass Ratio. Zeitschrift für Physik A Atoms and Nuclei, 297, 35-39. https://link.springer.com/article/10.1007/BF01414243
[51]	Van-Dyck, R.S., Moore, F.L., Farnham, D.L. and Schwinberg, P.B. (1985) New Measurement of the Proton-Electron Mass Ratio. International Journal of Mass Spectrometry and Ion Processes, 66, 327-337. https://doi.org/10.1016/0168-1176(85)80006-9
[52]	Becker, P. and Bettin, H. (2011) The Avogadro Constant: Determining the Number of Atoms in a Single-Crystal 28Si Sphere. Philosophical Transactions of the Royal Society A, 369, 3925-3935. https://doi.org/10.1098/rsta.2011.0222
[53]	Becker, P. (2012) The New Kilogram Definition Based on Counting the Atoms in a 28Si Crystal. Contemporary Physics, 53, 461-479. https://doi.org/10.1080/00107514.2012.746054
[54]	Bettin, H., Fujii, K., Man, J., Mana, G., Massa, E. and Picard, A. (2013) Accurate Measurements of the Avogadro and Planck Constants by Counting Silicon Atoms. Annalen der Physik, 525, 680-687. https://doi.org/10.1002/andp.201300038
[55]	Li, S.S., et al. (2014) Progress on Accurate Measurement of the Planck Constant: Watt Balance and Counting Atoms. Chinese Physics B, 24, Article ID: 010601. https://doi.org/10.1088/1674-1056/24/1/010601
[56]	Clotfelter, B.E. (1987) The Cavendish Experiment as Cavendish Knew It. American Journal of Physics, 55, 210. https://doi.org/10.1119/1.15214
[57]	Haug, E.G. (2021) Using a Grandfather Pendulum Clock to Measure the World’s Shortest Time Interval, the Planck Time (with Zero Knowledge of G). Journal of Applied Mathematics and Physics, 9, 1076-1088. https://doi.org/10.4236/jamp.2021.95074
[58]	Haug, E.G. (2021) Demonstration That Newtonian Gravity Moves At the Speed of Light and Not Instantaneously (Infinite Speed) as Thought! Journal of Physics Communication, 5, Article ID: 025005. https://doi.org/10.1088/2399-6528/abe4c8
[59]	Cornu, A. and Baille, J.B. (1873) Détermination nouvelle de la constante de l’attraction et de la densité moyenne de la terre. Comptes rendus de l’Académie des Sciences, 76, 954-957.
[60]	Boys, C.V. (1894) The Newtonian Constant of Gravitation. Nature, 50, 571. https://doi.org/10.1038/050571a0
[61]	Haug, E.G. (2022) Progress in the Composite View of the Newton Gravitational Constant and Its Link to the Planck Scale. Universe, 8, Article No. 454. https://doi.org/10.3390/universe8090454
[62]	Einstein, A. (1916) Näherungsweise integration der feldgleichungen der gravitation. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, Berlin.
[63]	Haug, E.G. (2016) Planck Quantization of Newton and Einstein Gravitation. International Journal of Astronomy and Astrophysics, 6, 206-217. https://doi.org/10.4236/ijaa.2016.62017
[64]	Haug, E.G. (2023) Different Mass Definitions and Their Pluses and Minuses Related to Gravity: The Kilogram Mass Is Likely Incomplete.
[65]	Haug, E.G. (2024) CMB, Hawking, Planck, and Hubble Scale Relations Consistent with Recent Quantization of General Relativity Theory. International Journal of Theoretical Physics, 63, Article No. 57. https://doi.org/10.1007/s10773-024-05570-6
[66]	Tatum, E.T., Seshavatharam, U.V.S. and Lakshminarayana, S. (2015) The Basics of Flat Space Cosmology. International Journal of Astronomy and Astrophysics, 5, 116-124. https://doi.org/10.4236/ijaa.2015.52015
[67]	Haug, E.G. and Wojnow, S. (2023) How to Predict the Temperature of the CMB Directly Using the Hubble Parameter and the Planck Scale Using the Stefan-Boltzman Law. Research Square. https://doi.org/10.21203/rs.3.rs-3576675/v1
[68]	Haug, E.G. and Tatum, E.T. (2023) The Hawking Hubble Temperature as a Minimum Temperature, the Planck Temperature as a Maximum Temperature and the CMB Temperature as Their Geometric Mean Temperature.
[69]	Hinkley, N., et al. (2013) An Atomic Clock with 10−18 Instability. Science, 341, 1215-1218. https://doi.org/10.1126/science.1240420
[70]	Bloom, B.J., et al. (2014) An Optical Lattice Clock with Accuracy and Stability at the 10−18 Level. Nature, 506, 71-75. https://doi.org/10.1038/nature12941
[71]	Nicholson, T.L., et al. (2015) Systematic Evaluation of an Atomic Clock at 2×10−18 Total Uncertainty. Nature Communication, 6, Article No. 6896. https://doi.org/10.1038/ncomms7896
[72]	Boulder Atomic Clock Optical Network (BACON) Collaboration (2021) Frequency Ratio Measurements at 18-Digit Accuracy Using an Optical Clock Network. Nature, 591, 564-569. https://doi.org/10.1038/s41586-021-03253-4
[73]	Haug, E.G. (2023) Different Mass Definitions and Their Pluses and Minuses Related to Gravity. Foundations, 3, 199-219. https://doi.org/10.3390/foundations3020017
[74]	Fixsen, D.J., et al. (2004) The Temperature of the Cosmic Microwave Background at 10 Ghz. The Astrophysical Journal, 612, 86-95. https://doi.org/10.1086/421993
[75]	Fixsen, D.J. (2009) The Temperature of the Cosmic Microwave Background. The Astrophysical Journal, 707, 916-920. https://doi.org/10.1088/0004-637X/707/2/916
[76]	Noterdaeme, P., Petitjean, P., Srianand, R., Ledoux, C. and López, S. (2011) The Evolution of the Cosmic Microwave Background Temperature. Astronomy and Astrophysics, 526, L7. https://doi.org/10.1051/0004-6361/201016140
[77]	Dhal, S., Singh, S., Konar, K. and Paul, R.K. (2023) Calculation of Cosmic Microwave Background Radiation Parameters Using COBE/FIRAS Dataset. Experimental Astronomy, 56, 715-726. https://doi.org/10.1007/s10686-023-09904-w
[78]	Friedmann, A. (1922) Über die Krüng des Raumes. Zeitschrift für Physik, 10, 377-386. https://doi.org/10.1007/BF01332580
[79]	Haug, E.G. (2021) Quantum Cosmology: Cosmology Linked to the Planck Scale.
[80]	Haug, E.G. (2022) Cosmological Scale versus Planck Scale: As above, So below! Physics Essays, 35, 356-363. https://doi.org/10.4006/0836-1398-35.4.356
[81]	Haug, E.G. (2024) The Extremal Universe Exact Solution from Einstein’s Field Equation Gives the Cosmological Constant Directly. Journal of High Energy Physics, Gravitation and Cosmology, 10, 386-397. https://doi.org/10.4236/jhepgc.2024.101027
[82]	Reissner, H. (1916) Über die eigengravitation des elektrischen feldes nach der einsteinschen theorie. Annalen der Physik, 355, 106-120. https://doi.org/10.1002/andp.19163550905
[83]	Nordström, G. (1918) On the Energy of the Gravitation Field in Einstein’s Theory. Koninklijke Nederlandsche Akademie van Wetenschappen Proceedings, 20, 1238.
[84]	Kerr, R.P. (1963) Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics. Physical Review Letters, 11, 237-238. https://doi.org/10.1103/PhysRevLett.11.237
[85]	Newman, E.T. and Janis, A.I. (1965) Note on the Kerr Spinning-Particle Metric. Journal of Mathematical Physics, 6, 915-917. https://doi.org/10.1063/1.1704350
[86]	Haug, E.G. and Spavieri, G. (2023) Mass-Charge Metric in Curved Spacetime. International Journal of Theoretical Physics, 62, Article No. 248. https://doi.org/10.1007/s10773-023-05503-9
[87]	Haug, E.G. and Spavieri, G. (2023) New Exact Solution to Einstein’s Field Equation Gives a New Cosmological Model.